SCML: Negotiate Your Way to Fornute

8 min readMay 1, 2021

In a previous article, I introduced the topic of automated negotiations and the International Automated Negotiating Agents Competition (ANAC) which will run as part of the official competitions track of IJCAI 2021 — one of the top AI conferences — this year. Winners will receive monetary prizes and will be announced during IJCAI.

This article focuses on the Supply Chain Management League (SCML) which runs as part of this competition.

SCML has three tracks this year:

OneShot A track focused on the problem of repeated concurrent negotiation.
Standard A track that combines the concurrent negotiation problem with effective long-term planning.
Collusion A track that focuses on methods that businesses can employ to corner the market.

OneShot is the simplest of these three tracks to explain. This article will focus exclusively on the SCML-OneShot game. In future articles, I will explain the main differences between the three tracks.

An overview of the SCML-OneShot game is available here and a full description for the details-savvy person is available here.

SCML has an online competition which allows you to compete against other participants before the official competition. Last year, this proved invaluable for improving agents and removing the worst of their bugs and unexpected behaviors by the time of the official competition.

A Simple-Enough Business-Like Game

Everything should be made as simple as possible, but no simpler, Albert Einstein.

The game simulates a common business environment in which factories (capable of running predefined manufacturing processes) try to maximize their profits through trade. There are exactly 3 products and 2 processes as shown in the figure. Each agent controls exactly one factory. All trade within the system is done through closed bilateral negotiations between agents and their suppliers. The market is driven by a set of exogenous contracts (non-negotiable) generated by the system every day (More on that later).

Game Participants develop these agents intending to maximize their profits in this competitive market.

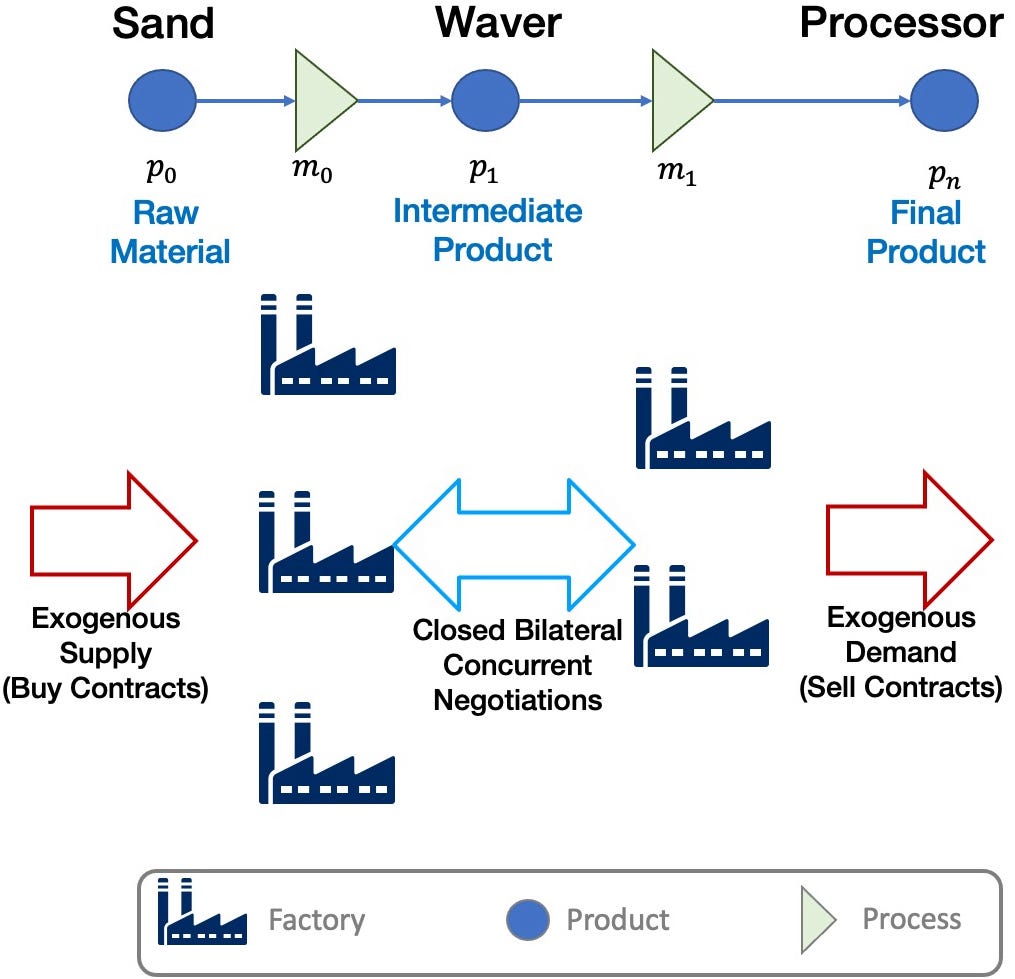
Agents that receive the raw material and generate the intermediate product are called L0 agents. Agents that receive the intermediate product and generate the final product are called L1 agents. The product type consumed by the factory controlled by an agent is called its input product and the product it produces is called its output product.

The simulation and utility function

Every day (simulation step), each L0 factory receives one exogenous contract specifying a quantity and a unit price (supplies of the raw material) for this day and each L1 factory receives one exogenous contract specifying a quantity and a unit price of the final product (sales) for the same day. Production and transportation are assumed to take no time.

L0 and L1 agents need to negotiate together to secure intermediate product contracts to use their supplies (for L0 agents) or satisfy their sale obligations (for L1 agents). All products that remain unsold at the end of the day perish (i.e. has no value). Moreover, agents pay a disposal cost for any input products they buy and never sell and pay a shortfall penalty for any sales they cannot satisfy.

Exogenous contracts drive the market. The profit of an agent can be calculated using a simple formula:

profit = revenue - supply cost - production cost - shortfall penalty - disposal
cost

Revenue comes from sales and is simply the total price of sell contracts executed by the agent (qout × pout). There are four sources of expenditure that should be minimized:

Supply Cost The total price of all buy contracts (qint × qin).
Production Cost The production cost per unit multiplied by the input quantity.
Shortfall Penalty A penalty paid for each item in the sell contracts not honored by the agent. For example, if the agent has an output contract with 5 but could only produce 3 items, it will pay this penalty for the remaining two (besides not receiving their price obviously).
disposal penalty A penalty paid for each item bought but not manufactured by the agent.

Considering this profit calculation for a moment, it is clear that the core problem facing the agent is to match its input and output quantities while maximizing the difference in their unit prices (for its advantage). Your goal as an agent designer is to maximize your overall profit over the simulation time.

The core problem targeted by SCML-OneShot is repeated concurrent negotiation with a known — yet variable — utility function.

Why is SCML-OneShot interesting?

SCML-OneShot is an incomplete information game because the payoffs (utility functions) are not common knowledge.

Moreover, automated negotiation in general is not a zero-sum game. This combination of a nonzero-sum incomplete information game is what makes SCML-OneShot interesting from the point of view of game theory.

Machine learning can be used in many ways in this game:

Learning about your partners. For example, try to estimate the utility function of your partner based on market conditions, past interactions with it, and its financial status.
Learning how to negotiate. An obvious method here is to employ RL with either self-play or playing against built-in agents provided by the organizers. You can then either adapt your learned policy in real-time or just use it as it is.
Learning to predict market conditions. For example, the changes in trading prices of the intermediate product can be important in devising an effective negotiation strategy.

We tried to set things up to make applying ML both effective and challenging:

The distribution of exogenous contracts between agents is not completely random, leading to similar utility functions for each agent on all days. This facilitates learning about partners.
The total demand in the market (total exogenous contract quantities and average prices) are common knowledge. This simplifies reasoning about the game and provides context information for ML methods.
The probability distributions from which game parameters are sampled are all described in the full game description.

How can I get started with SCML?

To get started, you need to install the scml package from PyPI:

pip install scml

You can then download the skeleton from the competition website.

Moreover, there is an optional visualization package scml-vis that helps you see what happens in simulations and tournaments. It is also pip installable:

pip install scml-vis

And you can use it to explore logs from game simulations:

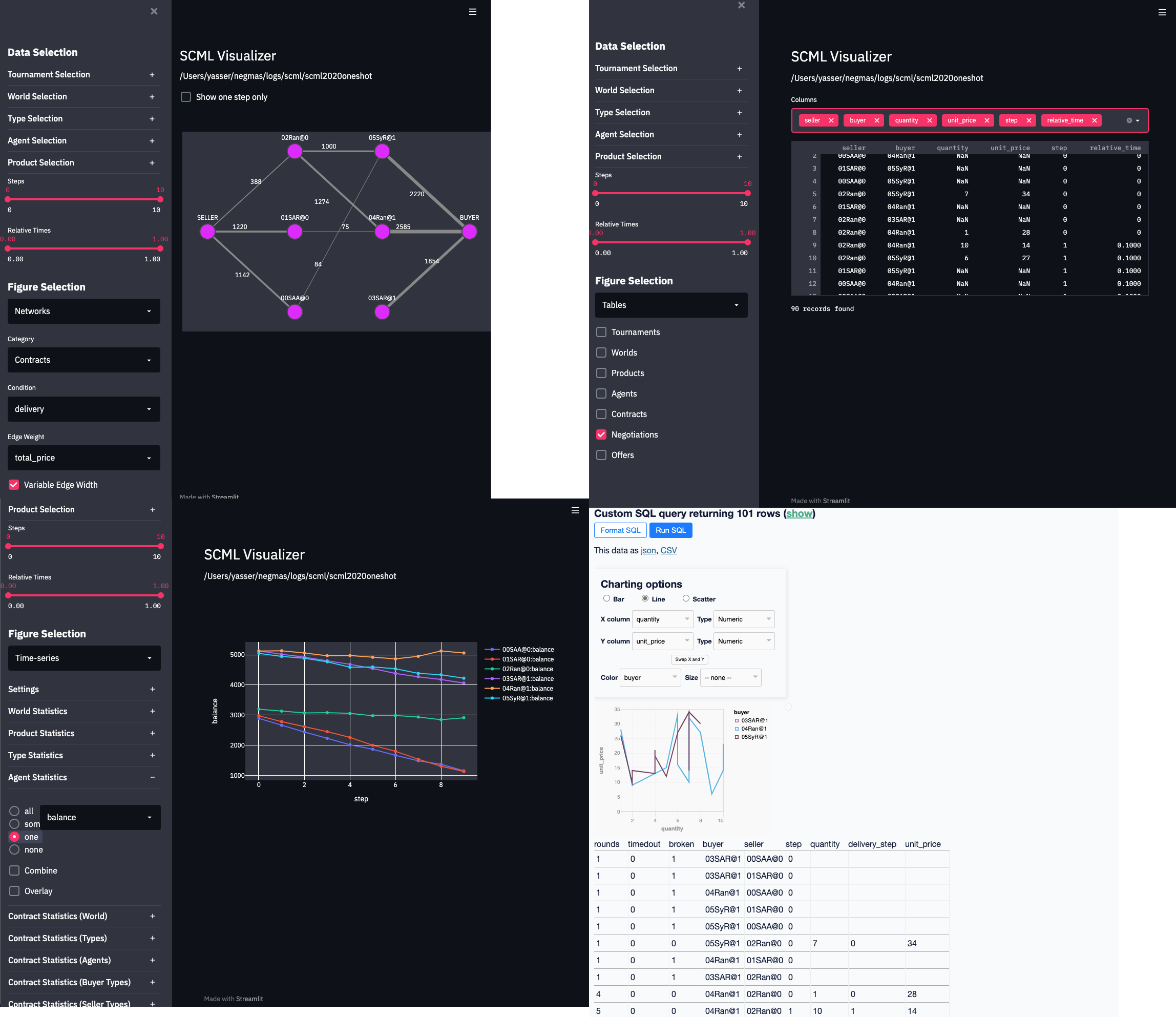
SCML-OneShot example visualization charts using scml-vis — SCML-OneShot example visualization charts using `scml-vis`

How difficult is it to develop an agent?

To develop an agent, you need to override two methods propose and respond for proposing and responding to offers from other agents. That is all folks 😎

Here is a complete agent. It is 34 lines of code.

class GreedyOneShotAgent(OneShotAgent):
    """A greedy agent based on OneShotAgent"""

    def init(self):
        self.secured = 0

    def step(self):
        self.secured = 0

    def on_negotiation_success(self, contract, mechanism):
        self.secured += contract.agreement["quantity"]

    def propose(self, negotiator_id: str, state) -> "Outcome":
        return self.best_offer(negotiator_id)

    def respond(self, negotiator_id, state, offer):
        my_needs = self._needed(negotiator_id)
        if my_needs <= 0:
            return ResponseType.END_NEGOTIATION
        return (
            ResponseType.ACCEPT_OFFER
            if offer[QUANTITY] <= my_needs
            else ResponseType.REJECT_OFFER
        )

    def best_offer(self, negotiator_id):
        my_needs = self._needed(negotiator_id)
        if my_needs <= 0:
            return None
        ami = self.get_ami(negotiator_id)
        if not ami:
            return None
        quantity_issue = ami.issues[QUANTITY]
        unit_price_issue = ami.issues[UNIT_PRICE]
        offer = [-1] * 3
        offer[QUANTITY] = max(
            min(my_needs, quantity_issue.max_value),
            quantity_issue.min_value
        )
        offer[TIME] = self.awi.current_step
        if self._is_selling(ami):
            offer[UNIT_PRICE] = unit_price_issue.max_value
        else:
            offer[UNIT_PRICE] = unit_price_issue.min_value
        return tuple(offer)

    def _needed(self, negotiator_id=None):
        return self.awi.current_exogenous_input_quantity + \
               self.awi.current_exogenous_output_quantity - \
               self.secured

    def _is_selling(self, ami):
        return ami.annotation["product"] == self.awi.my_output_product

world, ascores, tscores = try_agent(GreedyOneShotAgent)

The main idea of this agent is pretty simple. It tries to secure as much of its needs (sales/supplies) as possible in every negotiation at the best possible price for itself.

To achieve this goal, the agent keeps track of the quantity it secured in its init, step and on_negotiation_success callbacks.

def init(self):
    self.secured = 0

def step(self):
    self.secured = 0

def on_negotiation_success(self, contract, mechanism):
    self.secured += contract.agreement["quantity"]

Moreover, it defines a helper that calculates the amount it needs by subtracting the exogenous quantity it has from the amount it secured:

def _needed(self):
    return self.awi.current_exogenous_input_quantity + \
           self.awi.current_exogenous_output_quantity - \
           self.secured

Notice that either the exogenous input quantity or the exogenous output quantity (or both) will always be zero. Now that the agent can calculate how much it needs to buy/sell, it implements the negotiation related call-backs (propose and respond).

Here is the full implementation of propose:

def propose(self, negotiator_id: str, state) -> "Outcome":
        return self.best_offer(negotiator_id)

The agent is always offering its best offer which is calculated in the best_offer method to be discussed later. It does not concede at all.

Responding to opponent offers is also simple:

it starts by calculating its needs using the helper neededand ends the negotiation if it needs no more sales/supplies

my_needs = self._needed()
    if my_needs <= 0:
        return ResponseType.END_NEGOTIATION

If the offered quantity is less than its needs, accept the offer. Otherwise reject the offer.

return ResponseType.ACCEPT_OFFER if offer[QUANTITY] <= my_needs else ResponseType.REJECT_OFFER

Most of the code is in the best_offer method which calculates the best offer for a negotiation given the agreements reached so far. Let’s check it line by line:

The agent checks its needs and returns None ending the negotiation if it needs no more sales/supplies. We also get access to the AMI.

my_needs = self._needed()
    if my_needs <= 0:
        return None
    ami = self.get_ami(negotiator_id)
    if not ami:
        return None

It then finds out the Issue objects corresponding to the quantity and unit-price for this negotiation and initializes an offer (we have 3 issues)

quantity_issue = ami.issues[QUANTITY]
    unit_price_issue = ami.issues[UNIT_PRICE]
    offer = [-1] * 3

The time is always the current step.

offer[TIME] = self.awi.current_step

The quantity to offer is simply the needs of the agent without mapped within the range of the quantities in the negotiation agenda (note that this may lead the agent to buy more than its needs).

offer[QUANTITY] = max(
        min(my_needs, quantity_issue.max_value), quantity_issue.min_value
    )

Finally, the unit price is the maximum possible unit price if the agent is selling otherwise it is the minimum possible price. Note that is_selling() assumes that the agent will never find itself in a middle layer in a deep negotiation. We will alleviate this issue later.

if self._is_selling(ami):
        offer[UNIT_PRICE] = unit_price_issue.max_value
    else:
        offer[UNIT_PRICE] = unit_price_issue.min_value
    return tuple(offer)

This agent is extremely simplistic in several ways:

It insists on its price all the time making it too inflexible.
It accepts offers without even considering the price which makes it too gullible.
It does not even try to learn about its partners’ behavior during negotiation or over consecutive days.

To see examples of better agents, check the official tutorials

Online Competition and Available Resources

The online SCML competition is already open and will run until the beginning of July 2021. You can find all the details about the game, how to participate, and a wealth of tutorials and other resources on the competition website hosted by Brown University.

Summary

This article introduced the SCML-OneShot game which provides an interesting and novel challenge for the AI community. The competition (which runs as part of ANAC @ IJCAI 2021) is open to all.

Consider submitting to SCML and negotiate your way to fortune. Sorry!! Make your agent do that for you …